Note: This post was originally written in 2016 and imported from my old blog.

Binary search trees are a type of tree data-structure that store items in memory. Binary search trees (BST) keep their items in sorted order. Each child of the BST is also a tree and can have their own children. Each tree can have 0, 1, or 2 children.

The data starts off at the root of a tree, making comparisons to keys stored into the nodes of the tree and deciding to send the data left or right of the tree. If the value is lower than a node, it is assigned to the left and if it is greater, it is assigned to the right. If the node already has two children, it goes down one level and compares and adds to the children.

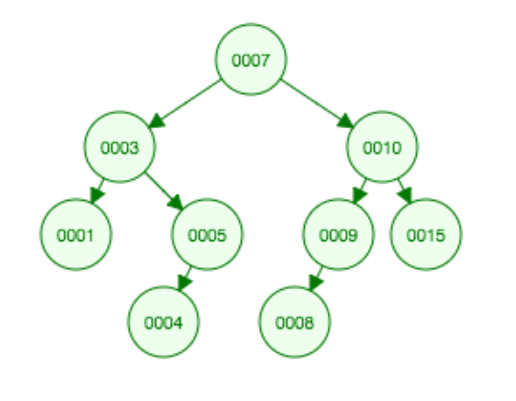
The above image was generated using:

https://www.cs.usfca.edu/~galles/visualization/BST.html

Because the data is essentially cut in half each time a left or right comparison is made, a BST is typically logarithmic lookup time (O(log n)) for inserting, searching, and deleting.

You can think of searching through a BST like looking in a dictionary for a word. Opening the dictionary on a random page to find the correct word, you either need to turn the pages to the right or to the left. If the beginning of the word comes before the words on your current page in the alphabet, you will need to look on the left side of where you currently are. Opening a random page on the left, you continue to look left or right until you correctly find the word. You also get closer with each step and ignore the rest of the dictionary. A BST is different than a dictionary as you will need to look according to the child nodes.

Traversing down tree structures will use recursion. Below is a function written in JavaScript on how you would traverse down a BST to see if the tree contains a value. It will return true if the value exists in the tree and false if not.

1binaryTree.contains = function(val) {
2  //Check if current node contains value
3  if (val === this.value) {
4    return true;
5  //if value is less than node value
6  } else if ( val < this.value ) {
7    //check nodes left value if it exists. 
8    //if not that means you have hit the end of the tree.
9    if (!this.left) {
10      return false;
11    //if left node exists, run contains recursively on that node
12    } else {
13      return this.left.contains(val);
14    }
15  } else if (val > this.value) {
16    //check nodes right value if it exists. 
17    //if not that means you have hit the end of the tree.
18    if (!this.right) {
19      return false;
20    //if right node exists, run contains recursively on that node
21    } else {
22      return this.right.contains(val);
23    }
24  }
25}